TensorFlow Quantum: 混合量子-经典机器学习 *¶
我们身边的经典计算机利用比特位和逻辑门进行二进制运算。在物理硬件上,这种运算主要是通过半导体的特殊导电性质实现的。经过几十年的发展,我们已经可以在一片小小的半导体芯片上集成上亿个晶体管,从而实现高性能的经典计算。
而量子计算(Quantum Computing)旨在利用具有量子特性(例如量子态叠加和量子纠缠)的“量子比特位”和“量子逻辑门”进行计算。这种新的计算模式可以在搜索和大数分解等重要领域达成指数级的加速,让当前无法实现的一些超大规模运算成为可能,从而可能在未来深远地改变世界。在物理硬件上,这类量子运算也可以通过一些具有量子特性的结构(例如超导约瑟夫森结)实现。
不幸的是,尽管量子计算的理论已经有了比较深入的发展,可在物理硬件上,我们目前仍然造不出一台超越经典计算机的通用量子计算机 1 。IBM和谷歌等业界巨头在通用量子计算机的物理构建上已经取得了一些成绩,但无论是量子比特的个数还是在退相干问题的解决上,都还远无法达到实用的层级。
以上是量子计算的基本背景,接下来我们讨论量子机器学习。量子机器学习的一种最直接的思路是使用量子计算加速传统的机器学习任务,例如量子版本的PCA、SVM和K-Means算法,然而这些算法目前都尚未达到可实用的程度。我们在本章讨论的量子机器学习则采用另一种思路,即构建参数化的量子线路(Parameterized Quantum Circuits, PQCs)。PQC可以作为深度学习模型中的层而被使用,如果我们在普通深度学习模型的基础上加入PQC,即称为混合量子-经典机器学习(Hybrid Quantum-Classical Machine Learning)。这种混合模型尤其适合于量子数据集(Quantum Data)上的任务。而TensorFlow Quantum正是帮助我们构建这种混合量子-经典机器学习模型的利器。接下来,我们会对量子计算的若干基本概念进行简介,然后介绍使用TensorFlow Quantum和谷歌的量子计算库Cirq构建PQC、将PQC嵌入Keras模型、并在量子数据集上训练混合模型的流程。
量子计算基本概念¶
本节将简述量子计算的一些基本概念,包括量子比特、量子门、量子线路等。
推荐阅读
如果你希望更深入地了解量子力学以及量子计算的基本原理,建议可以从以下两本书入手:
Hidary, Jack D. Quantum Computing: An Applied Approach . Cham: Springer International Publishing, 2019. https://doi.org/10.1007/978-3-030-23922-0. (注重代码实操的量子计算教程,GitHub上有配套源码: https://github.com/JackHidary/quantumcomputingbook )
量子比特¶
在二进制的经典计算机中,我们用比特(Bit,也称“位”)作为信息存储的基本单位,一个比特只有0或者1两种状态。而在量子计算机中,我们使用量子比特(Quantum Bit, Qubit,也称“量子位”)进行信息的表示。量子比特也有两种基本状态  和
和 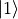 。不过量子比特除了可以处于这两种基本状态以外,还可以处于两者之间的叠加态(Superposition State),即
。不过量子比特除了可以处于这两种基本状态以外,还可以处于两者之间的叠加态(Superposition State),即 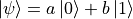 (其中a和b是复数,
(其中a和b是复数,  )。例如,
)。例如, 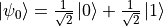 和
和 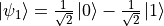 都是合法的量子态。我们也可以使用向量化的语言来表示量子比特的状态。如果我们令
都是合法的量子态。我们也可以使用向量化的语言来表示量子比特的状态。如果我们令 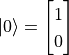 、
、 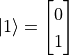 ,则
,则 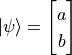 、
、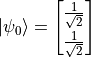 、
、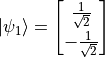 。
。
同时,我们可以用布洛赫球面(Bloch Sphere)来形象地展示单个量子比特的状态。球面的最顶端为  ,最底端为
,最底端为 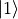 ,而从原点到球面上任何一点的单位向量都可以是一个量子比特的状态。
,而从原点到球面上任何一点的单位向量都可以是一个量子比特的状态。
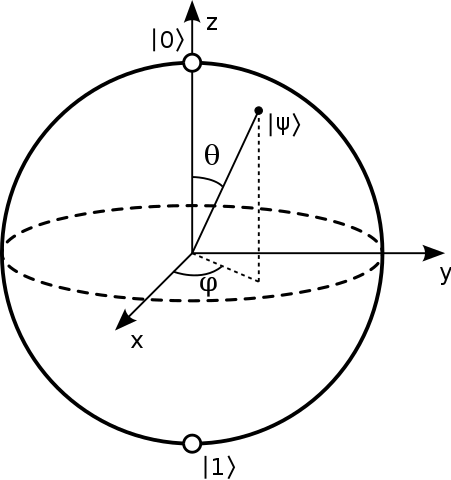
布洛赫球面( Bloch Sphere )。其中Z轴正负方向的量子态分别为基本态  和
和 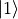 ,X轴正负方向的量子态分别为
,X轴正负方向的量子态分别为 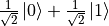 和
和 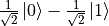 ,Y轴正负方向的量子态分别为
,Y轴正负方向的量子态分别为 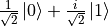 和
和 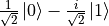 。图示来源¶
。图示来源¶
值得特别注意的是,尽管量子比特 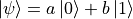 可能的状态相当之多,但一旦我们对其进行观测,则其状态会立即坍缩 2 到
可能的状态相当之多,但一旦我们对其进行观测,则其状态会立即坍缩 2 到  和
和 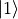 这两个基本状态中的一个,其概率分别为
这两个基本状态中的一个,其概率分别为 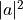 和
和 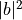 。
。
量子逻辑门¶
在二进制的经典计算机中,我们有AND(与)、OR(或)、NOT(非)等逻辑门,对输入的比特状态进行变换并输出。在量子计算机中,我们同样有量子逻辑门(Quantum Logic Gate,或简称“量子门”),对量子状态进行变换并输出。如果我们使用向量化的语言来表述量子状态,则量子逻辑门可以看作是一个对状态向量进行变换的矩阵。
例如,量子非门可以表述为 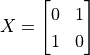 ,于是当我们将量子非门作用于基本态
,于是当我们将量子非门作用于基本态 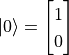 时,我们得到
时,我们得到 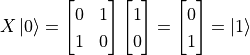 。量子门也可以作用在叠加态,例如
。量子门也可以作用在叠加态,例如 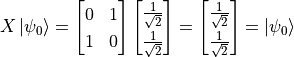 (这说明量子非门没能改变量子态
(这说明量子非门没能改变量子态 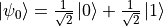 的状态。事实上,量子非门
的状态。事实上,量子非门 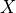 相当于在布洛赫球面上将量子态绕X轴旋转180度。而
相当于在布洛赫球面上将量子态绕X轴旋转180度。而 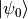 就在X轴上,所以没有变化)。量子与门和或门 3 由于涉及到多个量子位而稍显复杂,但同样可以通过尺寸更大的矩阵实现。我们会在后面讨论多量子位的情况。
就在X轴上,所以没有变化)。量子与门和或门 3 由于涉及到多个量子位而稍显复杂,但同样可以通过尺寸更大的矩阵实现。我们会在后面讨论多量子位的情况。
可能有些读者已经想到了,既然单个量子比特的状态不止  和
和 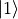 两种,那么量子逻辑门作为作为对量子比特的变换,其实也完全可以不局限于与或非。事实上,只要满足一定条件的矩阵 4 都可以作为量子逻辑门。例如,将量子态在布洛赫球面上绕X、Y、Z轴旋转的变换
两种,那么量子逻辑门作为作为对量子比特的变换,其实也完全可以不局限于与或非。事实上,只要满足一定条件的矩阵 4 都可以作为量子逻辑门。例如,将量子态在布洛赫球面上绕X、Y、Z轴旋转的变换 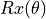 、
、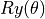 、
、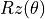 (其中
(其中 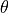 是旋转角度,当
是旋转角度,当 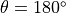 时记为
时记为 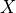 、
、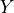 、
、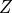 )都是量子逻辑门。另外,有一个量子逻辑门“阿达马门”(Hadamard Gate)
)都是量子逻辑门。另外,有一个量子逻辑门“阿达马门”(Hadamard Gate) 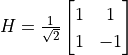 可以将量子状态从基本态转换为叠加态,在很多量子计算的场景中占据了重要地位。
可以将量子状态从基本态转换为叠加态,在很多量子计算的场景中占据了重要地位。
量子线路¶
当我们将量子比特以及量子逻辑门按顺序标记在一条或多条平行的线条上时,就构成了量子线路(Quantum Circuit,或称量子电路)。例如,对于我们在上一节讨论的,使用量子非门 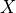 对基本态
对基本态  进行变换的过程,我们可以写出量子线路如下:
进行变换的过程,我们可以写出量子线路如下:
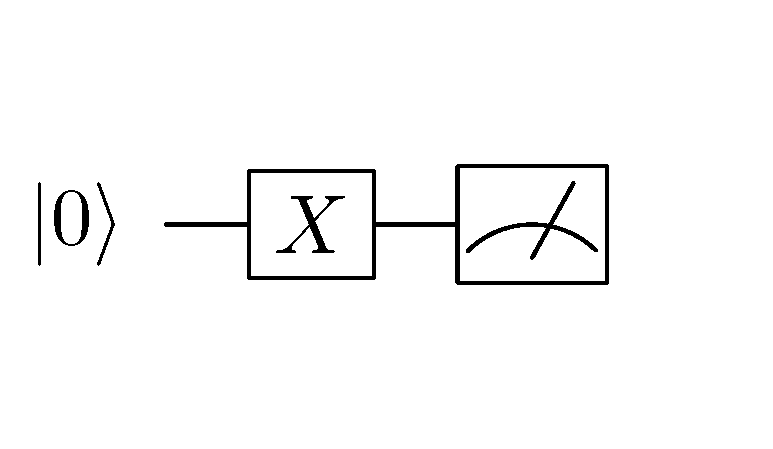
一个简单的量子线路¶
在量子线路中,每条横线代表一个量子比特。上图中最左边的  代表量子比特的初始态。中间的X方块代表量子非门
代表量子比特的初始态。中间的X方块代表量子非门 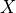 ,最右边的表盘符号代表测量操作。这个线路的意义是“对初始状态为
,最右边的表盘符号代表测量操作。这个线路的意义是“对初始状态为  的量子比特执行量子非门
的量子比特执行量子非门 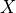 操作,并测量变换后的量子比特状态”。根据我们在前节的讨论,变换后的量子比特状态为基本态
操作,并测量变换后的量子比特状态”。根据我们在前节的讨论,变换后的量子比特状态为基本态 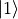 ,因此我们可以期待该量子线路最后的测量结果始终为1。
,因此我们可以期待该量子线路最后的测量结果始终为1。
接下来,我们考虑将上图中量子线路的量子非门 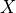 换为阿达马门
换为阿达马门 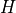 :
:
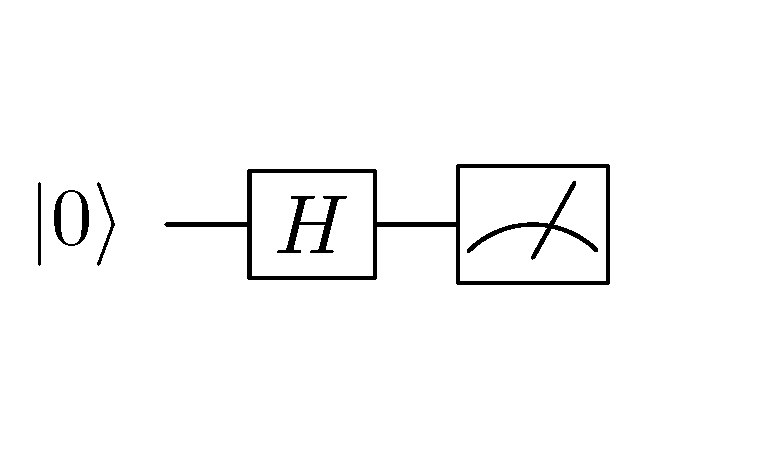
将量子非门 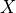 换为阿达马门
换为阿达马门 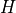 后的量子线路¶
后的量子线路¶
阿达马门对应的矩阵表示为 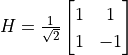 ,于是我们可以计算出变换后的量子态为
,于是我们可以计算出变换后的量子态为 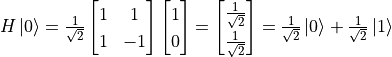 。这是一个
。这是一个  和
和 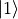 的叠加态,在观测后会坍缩到基本态,其概率分别为
的叠加态,在观测后会坍缩到基本态,其概率分别为 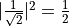 。也就是说,这个量子线路的观测结果类似于扔硬币。假若观测20次,则大约10次的结果是
。也就是说,这个量子线路的观测结果类似于扔硬币。假若观测20次,则大约10次的结果是  ,10次的结果是
,10次的结果是 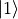 。
。
多比特的量子线路和量子纠缠 *¶
在上节中,我们讨论了基于单量子比特(两个基本态  和
和 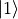 及其叠加)的量子逻辑门和量子线路。事实上,一个量子线路中可以出现多个量子比特,也有一些量子逻辑门能够以两个及以上的量子比特作为输入。
及其叠加)的量子逻辑门和量子线路。事实上,一个量子线路中可以出现多个量子比特,也有一些量子逻辑门能够以两个及以上的量子比特作为输入。
考虑具有两个量子比特的体系。一个量子比特具有2个基本态,则两个量子比特的体系具有 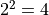 个基本态。我们可以将其以向量的形式写作
个基本态。我们可以将其以向量的形式写作
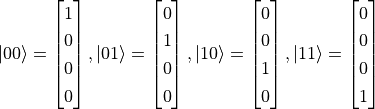
其中  代表第一和第二个量子比特均为基本态
代表第一和第二个量子比特均为基本态  ;
; 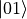 代表第一个量子比特为基本态
代表第一个量子比特为基本态  ,第二个量子比特为基本态
,第二个量子比特为基本态 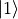 ,以此类推。
,以此类推。
假如我们有两个“独立”的量子比特 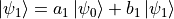 和
和 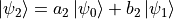 (
(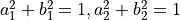 ),则由这两个量子比特组成的体系可以写作
),则由这两个量子比特组成的体系可以写作
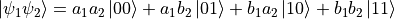
可以验证,该“联合”量子态坍缩到每个基本态的概率等于各量子比特坍缩到对应基本态的概率的乘积。例如,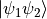 坍缩到
坍缩到  的概率是
的概率是 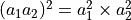 ,等于第一个量子比特坍缩到
,等于第一个量子比特坍缩到  的概率
的概率 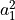 和第二个量子比特坍缩到
和第二个量子比特坍缩到  的概率
的概率 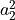 的乘积。同时,四个基本态的概率之和仍为1,即
的乘积。同时,四个基本态的概率之和仍为1,即 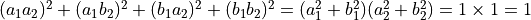 。这其实很类似于概率论中,两个独立随机变量的联合概率分布。
。这其实很类似于概率论中,两个独立随机变量的联合概率分布。
当然,正如同概率论中两个随机变量不一定独立,两个量子比特也不一定独立。对于 任意 的双量子比特体系 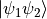 ,类似于单量子比特
,类似于单量子比特 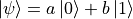 (其中
(其中  ),我们可以将其写作
),我们可以将其写作
![\ket{\psi_1\psi_2} = a \ket{00} + b \ket{01} + c \ket{10} + d \ket{11} = [a, b, c, d]^T](../../_images/math/e5fd087485dc9da5de76780563c8d0e7831f5ebd.png)
其中 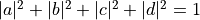 。对于给定的
。对于给定的 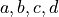 ,如果我们能找到一组
,如果我们能找到一组 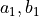 和
和 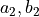 的值,使得
的值,使得 ![[a, b, c, d]^T = [a_1 a_2, a_1 b_2, b_1 a_2, b_1 b_2]^T](../../_images/math/4c0a68463fd866a3e3649e5d52b4cd552147e3af.png) 的话,我们称当前的联合量子态为“直积态”或“可分离态”。但是,这样的对应关系并不是总能建立的。例如,当
的话,我们称当前的联合量子态为“直积态”或“可分离态”。但是,这样的对应关系并不是总能建立的。例如,当 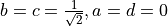 (即
(即 ![[0, \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}, 0]^T](../../_images/math/e9ab902b194086186fdd6e70378bfaa7b2e3838a.png) )时,则无法找到这样的对应关系。此时我们称当前的联合量子态为“纠缠态”。在这个例子中,联合量子态有
)时,则无法找到这样的对应关系。此时我们称当前的联合量子态为“纠缠态”。在这个例子中,联合量子态有  的概率坍缩到
的概率坍缩到 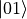 ,
, 的概率坍缩到
的概率坍缩到 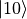 ,可见第一个量子比特和第二个量子比特是“纠缠”在一起的,“你坍缩到
,可见第一个量子比特和第二个量子比特是“纠缠”在一起的,“你坍缩到  则我坍缩到
则我坍缩到 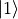 ,你坍缩到
,你坍缩到 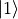 则我坍缩到
则我坍缩到  ”,两者有很强的相关性。
”,两者有很强的相关性。
不过,我们是不是真的可以获得这样的纠缠量子态呢?答案是肯定的。接下来,我们介绍一个重要的二元运算符CNOT(控制非门),其矩阵形式表示为
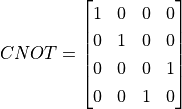
容易看出,这个运算符对于第一和第二个基本态  和
和 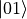 对应的系数
对应的系数 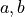 无作用,但会让第三和第四个基本态
无作用,但会让第三和第四个基本态 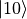 和
和 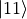 对应的系数
对应的系数 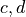 相互交换,即
相互交换,即 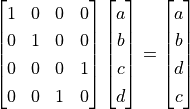 。例如,容易看出
。例如,容易看出 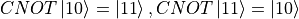 ,具体的表现,即“当第一个量子比特为
,具体的表现,即“当第一个量子比特为  时,第二个量子比特维持原样;当第一个量子比特为
时,第二个量子比特维持原样;当第一个量子比特为 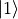 时,第二个量子比特取反”。这也是这个运算符被叫做“控制非门”的原因。这里,我们将第一个量子比特称作“控制比特”,第二个量子比特称作“目标比特”。
时,第二个量子比特取反”。这也是这个运算符被叫做“控制非门”的原因。这里,我们将第一个量子比特称作“控制比特”,第二个量子比特称作“目标比特”。
那么,回到之前的问题,如果我们想要制造形如 ![[0, \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}, 0]^T](../../_images/math/e9ab902b194086186fdd6e70378bfaa7b2e3838a.png) 的“纠缠”量子态,有了CNOT门之后,我们只需先制造
的“纠缠”量子态,有了CNOT门之后,我们只需先制造 ![[0, \frac{1}{\sqrt{2}}, 0, \frac{1}{\sqrt{2}}]^T](../../_images/math/e6493a5533f5d6f028c50d3f0fd6ba653051bade.png) ,然后让其通过CNOT门(即第3和第4个元素交换)即可。而
,然后让其通过CNOT门(即第3和第4个元素交换)即可。而 ![[0, \frac{1}{\sqrt{2}}, 0, \frac{1}{\sqrt{2}}]^T](../../_images/math/e6493a5533f5d6f028c50d3f0fd6ba653051bade.png) 是一个可分离态。容易验证,其可以通过两个独立的量子比特
是一个可分离态。容易验证,其可以通过两个独立的量子比特 ![[\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}]^T](../../_images/math/bd3761468f91b4e42ea298b5bc8a318421af7473.png) 和
和 ![[0, 1]^T](../../_images/math/0eeb975f4363f7e8e3a0285da8c0bbdef0471a7e.png) 组合而来。前者可以由基本态
组合而来。前者可以由基本态  通过阿达马门获得,后者即为基本态
通过阿达马门获得,后者即为基本态 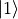 。由此,我们将第一个和第二个量子比特分别写在上下两条量子线路上,初始基本态分别为
。由此,我们将第一个和第二个量子比特分别写在上下两条量子线路上,初始基本态分别为  和
和 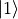 。第一个量子比特通过阿达马门,然后作为控制比特(
。第一个量子比特通过阿达马门,然后作为控制比特(  )连接到第二个量子比特,即“目标比特”上(
)连接到第二个量子比特,即“目标比特”上(  )。这里控制比特(
)。这里控制比特(  ),目标比特(
),目标比特(  )及其连线即代表了一个CNOT门。
)及其连线即代表了一个CNOT门。
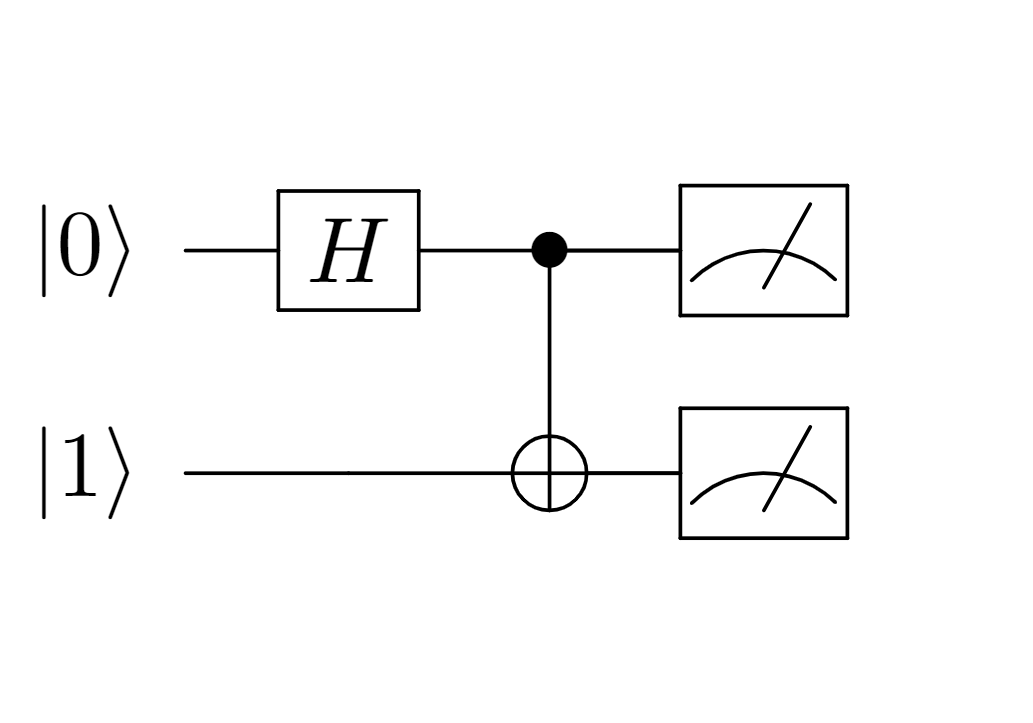
制造纠缠态的的量子线路¶
实例:使用Cirq建立简单的量子线路¶
Cirq 是谷歌主导的开源量子计算库,可以帮助我们方便地建立量子线路并模拟测量结果(我们在下一节介绍TensorFlow Quantum的时候还会用到它)。Cirq是一个Python库,可以使用 pip install cirq 进行安装。以下代码实现了上节所建立的两个简单的量子线路,并分别进行了20次的模拟测量。
import cirq
q = cirq.LineQubit(0) # 实例化一个量子比特
simulator = cirq.Simulator() # 实例化一个模拟器
X_circuit = cirq.Circuit( # 建立一个包含量子非门和测量的量子线路
cirq.X(q),
cirq.measure(q)
)
print(X_circuit) # 在终端可视化输出量子线路
# 使用模拟器对该量子线路进行20次的模拟测量
result = simulator.run(X_circuit, repetitions=20)
print(result) # 输出模拟测量结果
H_circuit = cirq.Circuit( # 建立一个包含阿达马门和测量的量子线路
cirq.H(q),
cirq.measure(q)
)
print(H_circuit)
result = simulator.run(H_circuit, repetitions=20)
print(result)
结果如下:
0: ───X───M───
0=11111111111111111111
0: ───H───M───
0=00100111001111101100
可见第一个量子线路的测量结果始终为1,第二个量子态的20次测量结果中有9次是0,11次是1(如果你多运行几次,会发现0和1出现的概率趋近于  )。可见结果符合我们在前节中的分析。
)。可见结果符合我们在前节中的分析。
同理,前节中制造纠缠态的双比特量子线路可以写作
import cirq
q_0, q_1 = cirq.LineQubit(0), cirq.LineQubit(1)
circuit = cirq.Circuit(
cirq.H(q_0),
cirq.X(q_1),
cirq.CNOT(q_0, q_1),
cirq.measure(q_0, key='q_0'),
cirq.measure(q_1, key='q_1')
)
print(circuit)
simulator = cirq.Simulator()
result = simulator.run(circuit, repetitions=20)
print(result)
结果如下:
0: ───H───@───M('q_0')───
│
1: ───X───X───M('q_1')───
q_0=11101110111101101101
q_1=00010001000010010010
这里由于cirq中的量子比特初始态为基本态  ,所以第二个量子比特首先通过一个量子非门转换为基本态
,所以第二个量子比特首先通过一个量子非门转换为基本态 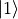 。从结果可见,第一个量子比特和第二个量子比特的测量结果始终相反,符合“纠缠”的特点。
。从结果可见,第一个量子比特和第二个量子比特的测量结果始终相反,符合“纠缠”的特点。
混合量子-经典机器学习¶
本节介绍混合量子-经典机器学习的基本概念,以及使用 TensorFlow Quantum 建立此类模型的方法。
在混合量子-经典机器学习过程中,我们使用量子数据集训练混合量子-经典模型。混合量子-经典模型的前半部分是量子模型(即参数化的量子线路)。量子模型接受量子数据集作为输入,对输入使用量子门进行变换,然后通过测量转换为经典数据。测量后的经典数据输入经典模型,并使用常规的损失函数计算模型的损失值。最后,基于损失函数的值计算模型参数的梯度并更新模型参数。这一过程不仅包括经典模型的参数,也包括量子模型的参数。具体流程如下图所示。
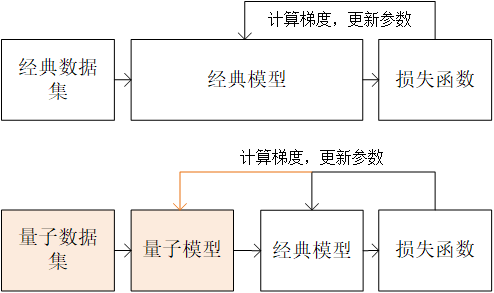
经典机器学习(上图)与混合量子-经典机器学习(下图)的流程对比¶
TensorFlow Quantum 即是一个与 TensorFlow Keras 结合紧密的,可快速建立混合量子-经典机器学习模型的开源库,可以使用 pip install tensorflow-quantum 进行安装。
后文示例均默认使用以下代码导入 TensorFlow、TensorFlow Quantum和Cirq:
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
推荐阅读
Broughton, Michael, Guillaume Verdon, Trevor McCourt, Antonio J. Martinez, Jae Hyeon Yoo, Sergei V. Isakov, Philip Massey, et al. “ TensorFlow Quantum: A Software Framework for Quantum Machine Learning. ” ArXiv:2003.02989 [Cond-Mat, Physics:Quant-Ph], March 5, 2020. (TensorFlow Quantum 白皮书)
量子数据集与带参数的量子门¶
以有监督学习为例,经典数据集由经典数据和标签组成。经典数据中的每一项是一个由不同特征组成的向量。我们可以将经典数据集写作 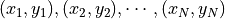 ,其中
,其中 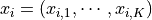 。量子数据集同样由数据和标签组成,而数据中的每一项是一个量子态。以前节单量子比特的量子态为例,我们可以将每一项数据写作
。量子数据集同样由数据和标签组成,而数据中的每一项是一个量子态。以前节单量子比特的量子态为例,我们可以将每一项数据写作 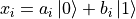 。在具体实现上,我们可以通过量子线路来生成量子数据。也就是说,每一项数据
。在具体实现上,我们可以通过量子线路来生成量子数据。也就是说,每一项数据 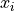 都对应着一个量子线路。例如,我们可以通过以下代码,使用Cirq生成一组量子数据:
都对应着一个量子线路。例如,我们可以通过以下代码,使用Cirq生成一组量子数据:
q = cirq.GridQubit(0, 0)
q_data = []
for i in range(100):
x_i = cirq.Circuit(
cirq.rx(np.random.rand() * np.pi)(q)
)
q_data.append(x_i)
在这一过程中,我们使用了一个带参数的量子门 cirq.rx(angle)(q) 。和之前我们使用的量子门 cirq.X(q) , cirq.H(q) 不同的是,这个量子门多了一个参数 angle ,表示将量子比特 q 绕布洛赫球面的x轴旋转 angle 角度(弧度制)。以上代码生成了100项量子数据,每项数据是从基本态  开始绕布洛赫球面的x轴随机旋转
开始绕布洛赫球面的x轴随机旋转 ![[0, \pi]](../../_images/math/b61438f8e15d426e93bf63b6c39c296435cdacaf.png) 弧度所变换而来的量子态。量子数据集在不少量子相关的领域(如化学、材料科学、生物学和药物发现等)都有应用。
弧度所变换而来的量子态。量子数据集在不少量子相关的领域(如化学、材料科学、生物学和药物发现等)都有应用。
当我们要将量子数据集作为Keras的输入时,可以使用TensorFlow Quantum的 convert_to_tensor 方法,将量子数据集转换为张量:
q_data = tfq.convert_to_tensor(q_data)
值得注意的是,当使用量子数据集作为Keras模型的训练数据时,Keras模型的输入类型( dtype )需要为 tf.dtypes.string 。
参数化的量子线路(PQC)¶
当我们在建立量子线路时使用了带参数的量子门,且该参数可以自由调整时,我们就称这样的量子线路为参数化的量子线路。Cirq支持结合SymPy这一Python下的符号运算库实现参数化的量子线路,示例如下
import sympy
theta = sympy.Symbol('theta')
q_model = cirq.Circuit(cirq.rx(theta)(q))
在上面的代码中,我们建立了如下图所示的量子线路。该量子线路可以将任意输入量子态 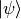 绕布洛赫球面的x轴逆时针旋转
绕布洛赫球面的x轴逆时针旋转 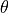 度,其中
度,其中 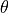 是使用
是使用 sympy.Symbol 声明的符号变量(即参数)。
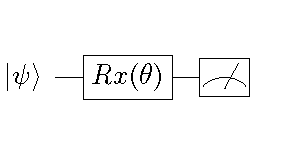
参数化的量子线路示例¶
将参数化的量子线路嵌入机器学习模型¶
通过TensorFlow Quantum,我们可以轻松地将参数化的量子线路以Keras层的方式嵌入Keras模型。例如对于前节建立的参数化的量子线路 q_model ,我们可以使用 tfq.layers.PQC 将其直接作为一个Keras层使用
q_layer = tfq.layers.PQC(q_model, cirq.Z(q))
expectation_output = q_layer(q_data_input)
tfq.layers.PQC 的第一个参数为使用Cirq建立的参数化的量子线路,第二个参数为测量方式,此处使用 cirq.Z(q) 在布洛赫球面的Z轴进行测量。
以上代码也可直接写作:
expectation_output = tfq.layers.PQC(q_model, cirq.Z(q))(q_data_input)
实例:对量子数据集进行二分类¶
在以下代码中,我们首先建立了一个量子数据集,其中一半的数据项为基本态  绕布洛赫球面的x轴逆时针旋转
绕布洛赫球面的x轴逆时针旋转 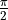 弧度(即
弧度(即 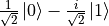 ),另一半则为
),另一半则为 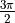 弧度(即
弧度(即 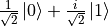 )。所有的数据均加入了绕x,y轴方向旋转的,标准差为
)。所有的数据均加入了绕x,y轴方向旋转的,标准差为 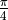 的高斯噪声。对于这个量子数据集,如果不加变换而直接测量,则所有数据都会和抛硬币一样等概率随机坍缩到基本态
的高斯噪声。对于这个量子数据集,如果不加变换而直接测量,则所有数据都会和抛硬币一样等概率随机坍缩到基本态  和
和 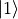 ,从而无法区分。
,从而无法区分。
为了区分这两类数据,我们接下来建立了一个量子模型,这个模型将单比特量子态绕布洛赫球面的x轴逆时针旋转 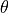 弧度。变换过后量子态数据的测量值送入“全连接层+softmax”的经典机器学习模型,并使用交叉熵作为损失函数。模型训练过程会自动同时调整量子模型中
弧度。变换过后量子态数据的测量值送入“全连接层+softmax”的经典机器学习模型,并使用交叉熵作为损失函数。模型训练过程会自动同时调整量子模型中 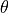 的值和全连接层的权值,使得整个混合量子-经典机器学习模型的准确度较高。
的值和全连接层的权值,使得整个混合量子-经典机器学习模型的准确度较高。
import cirq
import sympy
import numpy as np
import tensorflow as tf
import tensorflow_quantum as tfq
q = cirq.GridQubit(0, 0)
# 准备量子数据集(q_data, label)
add_noise = lambda x: x + np.random.normal(0, 0.25 * np.pi)
q_data = tfq.convert_to_tensor(
[cirq.Circuit(
cirq.rx(add_noise(0.5 * np.pi))(q),
cirq.ry(add_noise(0))(q)
) for _ in range(100)] +
[cirq.Circuit(
cirq.rx(add_noise(1.5 * np.pi))(q),
cirq.ry(add_noise(0))(q)
) for _ in range(100)]
)
label = np.array([0] * 100 + [1] * 100)
# 建立参数化的量子线路(PQC)
theta = sympy.Symbol('theta')
q_model = cirq.Circuit(cirq.rx(theta)(q))
# 建立量子层和经典全连接层
q_layer = tfq.layers.PQC(q_model, cirq.Z(q))
dense_layer = tf.keras.layers.Dense(2, activation=tf.keras.activations.softmax)
# 使用Keras建立训练流程。量子数据首先通过PQC,然后通过经典的全连接模型
q_data_input = tf.keras.Input(shape=() ,dtype=tf.dtypes.string)
expectation_output = q_layer(q_data_input)
classifier_output = dense_layer(expectation_output)
model = tf.keras.Model(inputs=q_data_input, outputs=classifier_output)
# 编译模型,指定优化器、损失函数和评估指标,并进行训练
model.compile(
optimizer=tf.keras.optimizers.SGD(learning_rate=0.01),
loss=tf.keras.losses.sparse_categorical_crossentropy,
metrics=[tf.keras.metrics.sparse_categorical_accuracy]
)
model.fit(x=q_data, y=label, epochs=200)
# 输出量子层参数(即theta)的训练结果
print(q_layer.get_weights())
输出:
...
200/200 [==============================] - 0s 165us/sample - loss: 0.1586 - sparse_categorical_accuracy: 0.9500
[array([-1.5279944], dtype=float32)]
可见,通过训练,模型在训练集上可以达到95%的准确率, 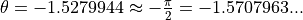 。而当
。而当 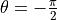 时,恰好可以使得两种类型的数据分别接近基本态
时,恰好可以使得两种类型的数据分别接近基本态  和
和 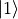 ,从而达到最易区分的状态。
,从而达到最易区分的状态。